Doğal sayıların yapımı
Peano Belitleri tanımı
Peano belitleri tarihsel olarak doğal sayıların en genel (ve sezgisel) tanımıdır. Modern tanımlar bu tanımı sağlar.
- Sıfır bir doğal sayıdır.
- Her doğal sayının, yine bir doğal sayı olan bir ardılı vardır.
- Ardılı sıfır olan hiç bir doğal sayı yoktur.
- Ardılları eşit olan doğal sayılar da birbirine eşittir.
- Doğal sayılardan oluşan bir küme, sıfırı ve her doğal sayının ardılını içeriyorsa o küme doğal sayılar kümesine eşittir.
Sıfırı doğal sayı olarak kabul etmeyen grup, buradaki belitlerin birincisini "Bir, bir doğal sayıdır." olarak kabul eder.
Zermelo-Freankel küme kuramı) doğal sayılar, von Neumann sıral sayılarıyla inşa edilebilir. Buna göre her sayı temelde bir kümedir. Eğer sıfır boşküme olarak tanımlanırsa ve her n sayının ardılı, n + , n {n} olarak verilirse, doğal sayılar inşa edilmiş olur.
{n} olarak verilirse, doğal sayılar inşa edilmiş olur.

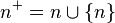
Bu tanım doğal sayıların yinelgen bir yapıda olduğunu da belirtmiş olur. Bu yinelgen tanımla sayılar,
- 0={}
- 1={0}
- 2={0,1}
- 3={0,1,2}
- ...
- n+1={0,1,...,n}
Bu tanımda iki doğal sayının eşitliği sayıların öğe sayısına dayanır.
Russell'ın farklı bir tanımı daha genel görünebilir:0 DOĞAL SAYIDIR
 (sıfır, hiç öğesi olmayan tüm kümelerin kümesi)
(sıfır, hiç öğesi olmayan tüm kümelerin kümesi)  (n nin ardılı, öğe sayısı n olan tüm kümelerin kümesi)
(n nin ardılı, öğe sayısı n olan tüm kümelerin kümesi)
Ne var ki bu tanım belitsel küme kuramlarında geçerli değildir, çünkü bir sayı, küme olamayacak kadar büyük topluluklar olmak zorunda kalıyor. Ancak tipler kuramı gibi kuramlarda geçerlidir.
Büyüklük ve küçüklük ilişkileri [değiştir]
Doğal sayıların karşılaştırılmasına en büyük basamaktan başlanır. Aynı basamakta büyük rakamı bulunan sayı diğerinden büyüktür.
İki sayının yüz milyonlar basamaklarında eşit rakamlar bulunuyor. Bu nedenle karşılaştırma bir sonraki basamak olan on milyonlar basamaklarında yapılır. Bu basamaklarda 9 > 8 olduğundan 894.125.067 > 887.954.700 yazılır. “ 894.125.067 büyüktür 887.954.700 şeklinde okunur.”
N = {0,1,2,3,4,5,...} Doğal Sayılar Kümesinde; iki doğal sayının toplamı yine bir doğal sayı olur.
Doğal sayılarda işlemler [değiştir]
Toplama işlemi [değiştir]
Toplama işlemi ileri doğru sayma işlemidir. Toplama işlemine katılan sayılara terim, işlemin sonucuna toplam denir. Toplama işlemi sayıların aynı basamakları arasında yapılır. Bu nedenle toplama işleminde sayılar aynı basamaklar alt alta gelecek şekilde yazılır.
Doğal sayılarda toplama aşağıdaki cebirsel kurallara uyar:
- a + 0 = a
- a + b = b + a
- (a + b) + c = a + (b + c)
- (a + b)c = ac + bc
Bir a sayısını bir b sayısıyla toplamak, a sayısının b kere ardılını almak olarak tanımlanır. Daha matematiksel bir tanım verilmek istenirse Ard(n) gösterimi n sayısının ardılını ifâde etmek üzere, toplama aşağıdaki belitlerle tanımlanır:
- a + 0 = a
- a + Ard(b) = Ard(a + b)
Bu belitlerden yola çıkarak ardıllık işlemini toplama cinsinden göstermek mümkündür: 2. belitte b=0 seçilirse
- a + Ard(0) = ard(a + 0)
sıfırın adrılı birdir, o halde,
- Ard(a) = a + 1
olduğu kolaylıkla görülür.
Çarpma işlemi art arda toplama işlemidir. Çarpma işlemine katılan sayılara çarpan, işlemin sonucuna çarpım denir.
Doğal sayılarda çarpma aşağıdaki cebirsel kurallara uyar:
- a1 = a
- ab = ba
- (ab)c = a(bc)
- c(a + b) = ca + cb
Bir a sayısını bir b sayısıyla çarpmak, a sayısının b kere toplamını almak olarak tanımlanır. Daha matematiksel bir tanım verilmek istenirse Ard(n) gösterimi n sayısının ardılını ifâde etmek üzere, çarpma aşağıdaki belitlerle tanımlanır:
- a1 = a




